What is the longest known sequence of numbers that repeats in Pi?

Have you ever wondered what numbers repeat in the known decimal representation of Pi? A quick look at Pi reveals a few obvious answers:

3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094330572703657595919530921861173819326117931051185480744623799627495673518857527248912279381830119491298336733624406566430860213949463952247371907021798609437027705392171762931767523846748184676694051320005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235420199561121290219608640344181598136297747713099605187072113499999983729780499510597317328160963185950244594553469083026425223082533446850352619311881710100031378387528865875332083814206171776691473035982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989380952572010654858632788659361533818279682303019520353018529689957736225994138912497217752834791315

The first and most obvious repeat is a single digit, 1, which repeats in the first 3 digits of Pi.

3.1415926535897932384626433832

Looking a bit deeper, we can see that the 2 digit number 26 repeats pretty quickly, at locations 6 and 21.

3.1415926535897932384626433832

How about 3, or 4, or 5 digits? Check!

• 592 occurs at position 4 and 61
• 0582 occurs at position 50 and 132
• 60943 occurs at 397 and 551

How far does this rabbit hole go? It turns out these numbers are represented in a sequence in the OEIS (Online Encyclopedia of Integer Sequences) A197123.

This series shows the repeating numbers calculated up to 18 digits in length. The last number in the series, 013724950651727463 occurs in Pi at locations 378,355,223 and 1,982,424,643. As you add additional digits to the search, the number of digits of Pi you will need to search goes up … so this sequence gets difficult quickly!

Can we do better? Can we find the next numbers in the sequence? Lets start by taking a crack at an algorithm in Python.

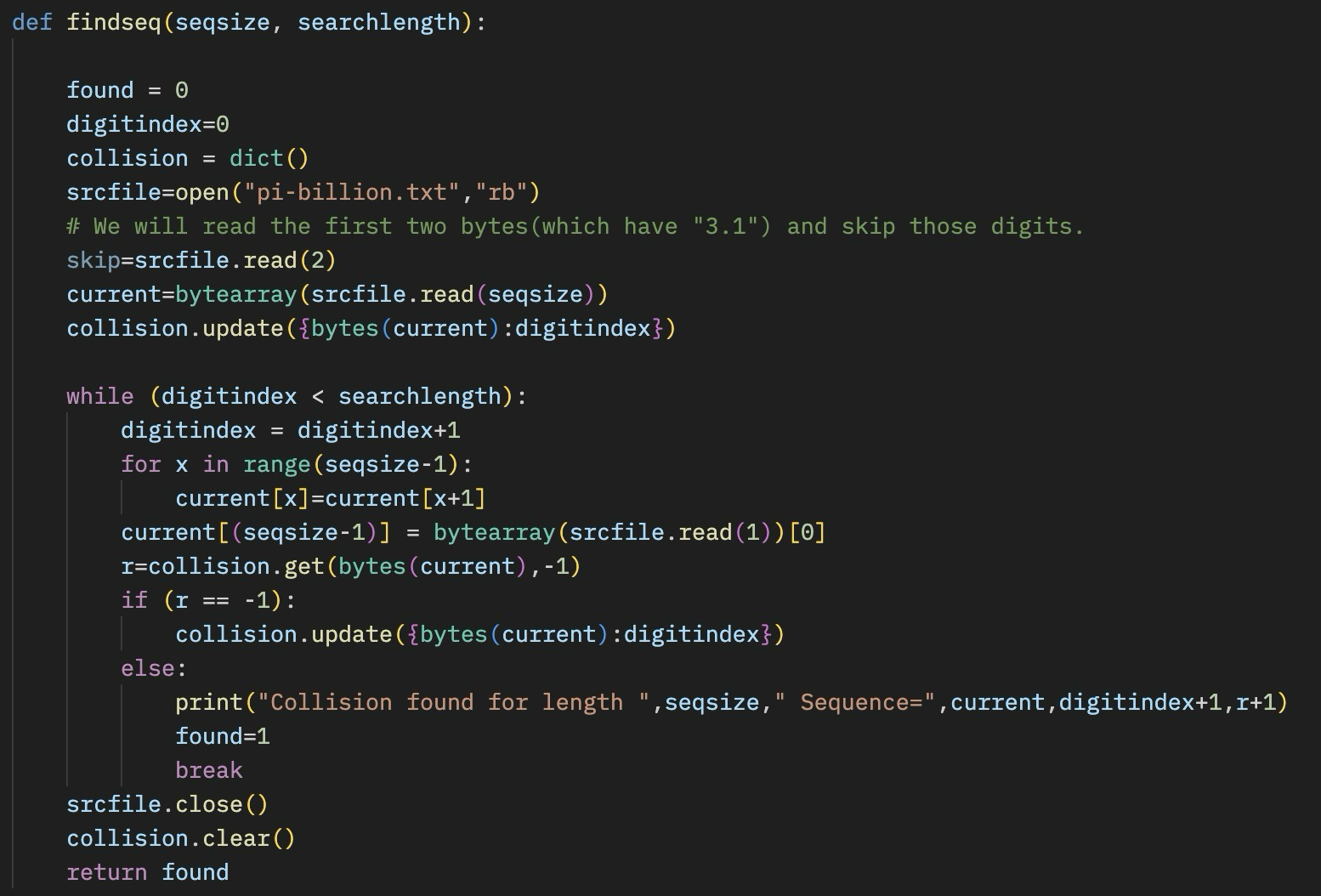
It is a pretty easy task to do using the built in ‘Dictionary‘ type, as that type will tell you if you insert an object that is a duplicate. It also is ordered, and uses a dynamic hash table of lists which works well for this kind of problem. We simply iterate through all of the digits of pi stored in a file (pi-billion.txt), and insert each of those numbers into a dictionary. If there is a collision we have found the number we are looking for. We also insert into the dictionary the location of the number in Pi.

If we use 100 million digits of Pi, we can pretty quickly find the first 17 numbers in this sequence, but the 18th entry does not occur in the first 900 million digits.

python3 seqinpi.py 900000000
Seaching using 900000000 digits of Pi
Collision found for length  2  Sequence= bytearray(b'26') 21 6
  Compute Time: 0.0 s
Collision found for length  3  Sequence= bytearray(b'592') 61 4
  Compute Time: 0.0 s
Collision found for length  4  Sequence= bytearray(b'0582') 132 50
  Compute Time: 0.0 s
Collision found for length  5  Sequence= bytearray(b'60943') 551 397
  Compute Time: 0.001 s
Collision found for length  6  Sequence= bytearray(b'949129') 1296 496
  Compute Time: 0.001 s
Collision found for length  7  Sequence= bytearray(b'8530614') 4601 4167
  Compute Time: 0.003 s
Collision found for length  8  Sequence= bytearray(b'52637962') 15434 15052
  Compute Time: 0.012 s
Collision found for length  9  Sequence= bytearray(b'201890888') 33844 30627
  Compute Time: 0.022 s
Collision found for length  10  Sequence= bytearray(b'4392366484') 240479 182105
  Compute Time: 0.156 s
Collision found for length  11  Sequence= bytearray(b'89879780761') 694399 550497
  Compute Time: 0.509 s
Collision found for length  12  Sequence= bytearray(b'756130190263') 857982 447673
  Compute Time: 0.665 s
Collision found for length  13  Sequence= bytearray(b'3186120489507') 5563712 3143598
  Compute Time: 4.972 s
Collision found for length  14  Sequence= bytearray(b'18220874234996') 9289694 4821309
  Compute Time: 8.784 s
Collision found for length  15  Sequence= bytearray(b'276854551127715') 28048917 19552188
  Compute Time: 28.441 s
Collision found for length  16  Sequence= bytearray(b'8230687217052243') 129440088 67889102
  Compute Time: 139.241 s
Collision found for length  17  Sequence= bytearray(b'93415455347042966') 262527966 109303021
  Compute Time: 295.78 s

The search for the last number did not complete because I ran out of memory on my 64GB Mac M1. Clearly to find these bigger numbers we are going to need a more efficient method, and a lot more ram!

I have a small homelab (https://www.youtube.com/watch?v=-b3t37SIyBs), and in that homelab I have math compute cluster that has 4 machines and each machine has 768GBs of RAM. I could just run the python code on those machines, but it turns out the Python implementation of the dictionary is not very memory efficient for this specific use case. I need to do better and faster.

I figured a faster way to do that was to write something in C. It would be portable, quick and easy to write, and fast. I wanted something simple and optimized, so elegant and refactorable code design was not on the menu. (The cool kids would do this in assembly btw, but that would take more time for sure to write!) No error checking either! If it crashes, that is the answer.

I decided to use a structure much like the Python Dictionary – A hash table where each hash entry points to a list of candidate numbers. If the hash table is big enough, the lists will never get very long. It is also worthwhile to insert numbers into the ‘lists’ ordered, as that will make searching the list faster.

I started with a simple struct for a candidate number:



For every number I am going to test against I would create one of these. It has a fixed length buffer for the number to test, the offset in Pi where that number occurs, and a pointer to another of these structures to make a list. It would be possible to optimize this by not using a byte per digit – we could pack two digits into a byte BCD style without a lot more work. If we start getting close to our memory limit we will give that a shot.

The ‘number’ stored in the ‘num’ array is directly as read from the pi-billions.txt file, so they are ASCII offsets. We could subtract ‘0’ from these so they are simple byte values, but it doesn’t make large difference in execution time. If the loop time becomes the bottleneck there are clear optimization to be done here.

The top level table is just a big array of pointers. For starters lets use a hash table that has 20 billion entries. 20 billion pointers will use up 160GBs of RAM. My source file for digits of Pi has 1 trillion digits, so I have plenty of room to grow this.




That will take a few seconds to run, and once it is done we will clear out the entries and start our search.
The code that does the search is simple:

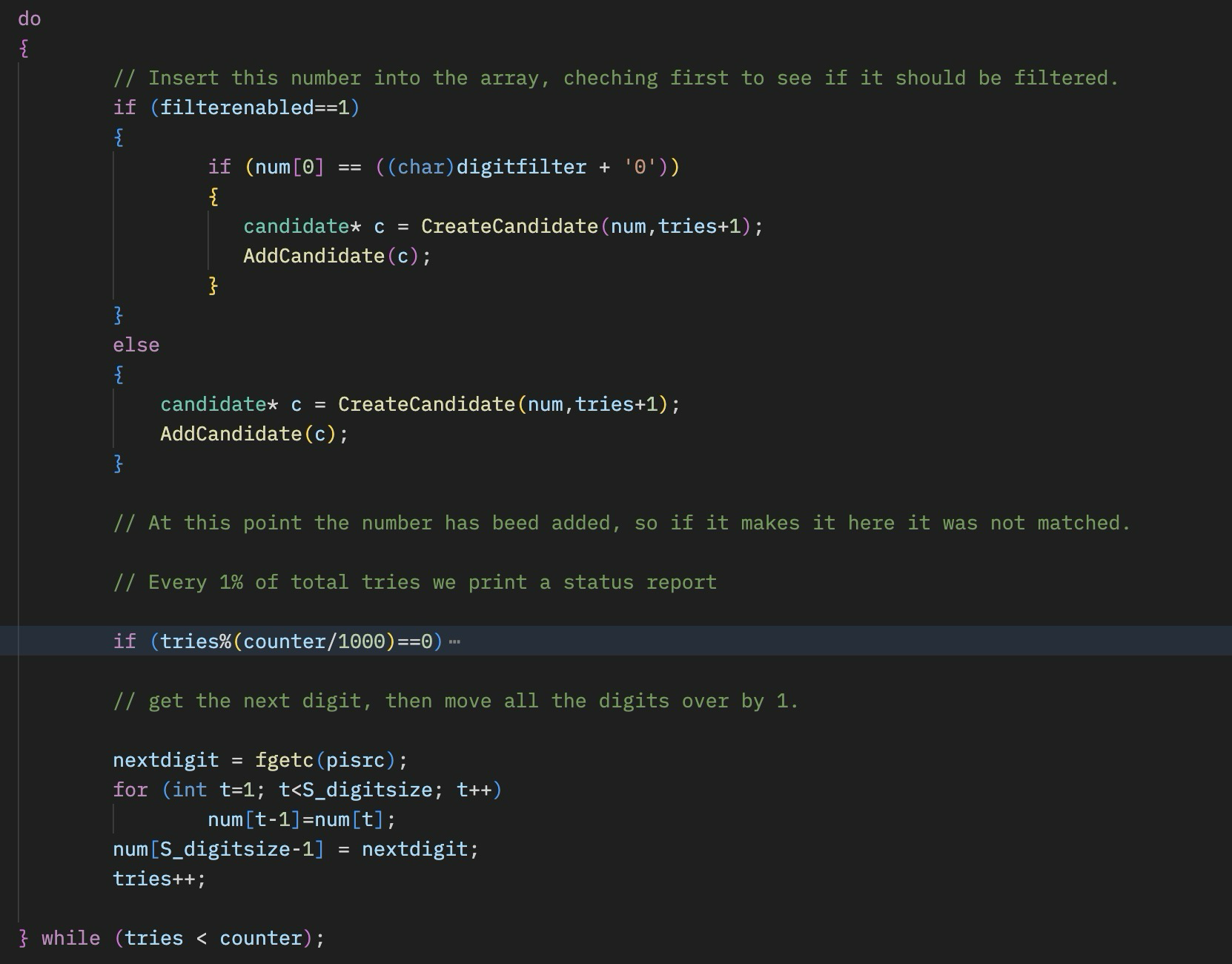
It created a candidate number, adds it to the structure, then loops. There is one optimization that is added here – the ability to filter the starting digit. The idea is that we want to be able to run through all 100 billion digits of Pi, but only test the numbers that start with a specific digit. That enables us to break down the problem into 10 smaller pieces that can each be do independently. It also cuts the memory use by a factor of 10, so it gives us 10 times more range. This same technique could be expanded to more than one digit to create more divisions of work. This is ideal for limited memory operations! You can always just run the numbers in sequence on the same machine.

One interesting consideration is how to calculate a hash quickly that will spread out across all of the numbers that we are sorting. Since they are numbers that have an even distribution in the ‘random’ nature of Pi, we can just use the first N digits of the numbers to pick the hash location.

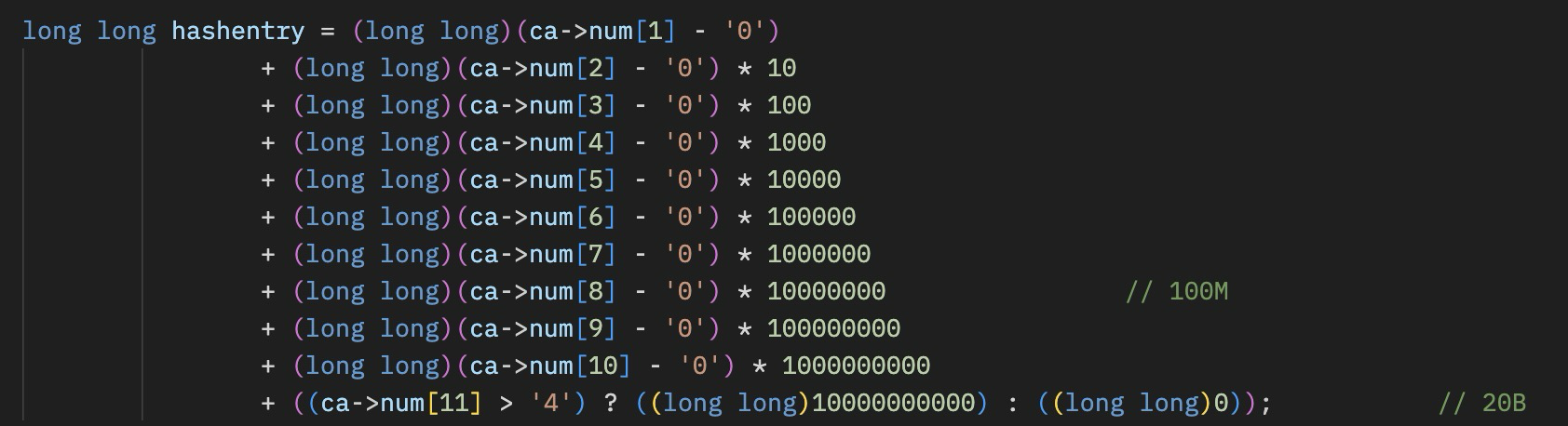
With the hash calculated, a simple walk of the list at that hash location will find a match or the location for insertion. This entire process could be optimized significantly with some better inline code, a reduction in math operations, and some memory footprint tweaking.

However it is on the whole pretty fast.. and most of all it can do larger searches. My first goal was to confirm the current largest entry from OEIS – the 18 digit number 013724950651727463. The first parameter is the number of digits of Pi to search in millions, second is the sequence length to look for.

./seqhash 2000 18
Match found! 013724950651727463 = 013724950651727463
Locations: 1982424643,378355223
Search Complete
Current Element Count: 1982.42 M   - Execution took 1239948 ms
Calculating Statistics
18112652634 empty hashes out of 20000000000 total hash entries.

That took 20 mins to execute, but only used 10% of the hash table. Time to set some records! Let’s take a crack at a 19 digit number. Based on the distribution it will probably be in the first 10 billion digits of Pi, so we will start searching there.

*******Match found! 1350168131352524443 = 1350168131352524443
Locations: 8858170606,4750253204
Search Complete
Current Element Count: 8858.17 M   - Execution took 4975300 ms
Calculating Statistics
12843333674 empty hashes out of 20000000000 total hash entries.

Bingo! The 19th in the series occurs at 4.7b and 8b digit locations. This took 82 mins, searching up to 8.8 billion digits. Next up lets try for the 20th. We are going to need to search more digits, as the 20th probably falls in the 10-100 billion digits. Let’s start by searching the first 20 billion digits. With a hash table that is 160GB in memory size, the 20 billion numbers would take up 800GBs of memory, so more memory than is available. To solve this, we will run the search 10 times with a different starting digit each time. That will make each search only 2 billion numbers (80GBs+160GB Hash table), so plenty of headroom. Since I have 4 compute nodes, I can run the search on all four at the same time.

Match found! 84756845106452435773 = 84756845106452435773
Locations: 17601613331,15494062638
Search Complete
Current Element Count: 1760.16 M   - Execution took 4296096 ms
Calculating Statistics
18315064429 empty hashes out of 20000000000 total hash entries.

Success! It took nine runs starting with digit 0, but on digit 8 a match was found. To be sure there was not another match that was earlier the 9 digit was also ran. Each digit run took ~70 mins for a total execution time of 700 mins (~12 hours). Not bad for finding a needle in the Pi haystack.

This lead to the obvious question – can we find element 21? Let’s give it a try! I will start by running against the first 100 billion digits of Pi, using the split into 10 filtering. Each run will be 10 billion digits, so ram use will be (400GB + 160GB) 560GBs, well within the capability of this hardware.

Winner Winner, we have a number:

Match found! 585270898631522188621 = 585270898631522188621
Locations: 69658148238,5644388308
Search Complete
Current Element Count: 6965.77 M   - Execution took 9006772 ms

This search was a bit faster, but the other 9 searches took about 3 hours each for a total compute time of 34 hours. During the search I actually found a 2 more 21 digit repeated number:

Match found! 685151818447609104295 = 685151818447609104295
Locations: 95098922518,2126170845
Search Complete
Current Element Count: 9509.71 M   - Execution took 14254387 ms

***Match found! 953657151565326368763 = 953657151565326368763
Locations: 99532319752,61194089794
Search Complete
Current Element Count: 9953.19 M   - Execution took 12114160 ms
Calculating Statistics
12159046679 empty hashes out of 20000000000 total hash entries.

Both of these numbers occurs for the second time farther into the digits of Pi, but the first occurrence is closer than the 58xx number for one of them! By definition of this series the first number (585270898631522188621) is considered the 21st element in the series since it completes the pair first.

Finding the next number (length 22) will take a bit more work. We will start by searching the first 200 billion digits, on the hope it is there somewhere. As before the work will be divided up into 10 subsections, starting with numbers that start with 0,1,2… up to 9. After about 8 hours the ‘1’ thread popped up a solution:

*****Match found! 1587124362959858673273 = 1587124362959858673273
Locations: 132915426432,107265929645
Search Complete
Current Element Count: 13291.46 M   - Execution took 14476959 ms

********Match found! 2761994111668451704865 = 2761994111668451704865
Locations: 122027419722,73134869029
Search Complete
Current Element Count: 12202.81 M   - Execution took 15186598 ms
Calculating Statistics
10865492760 empty hashes out of 20000000000 total hash entries.

The second number (2761994111668451704865) is the first one to show up twice, so that is the next number in the series. That second occurrence occurs at 122 billion digits, but the first occurence occurs at 73 billion digits.

The quest for the 23 digit number will take a bit more work as a searching up to 200 billion digits is about the limit in a 1/10 pass with the system ram I have. I have a new machine with 1.5TB on the way and that will accelerate the search.

If you like these kinds of puzzles I highly recommend you watch the Youtube channel Numberphile (https://www.youtube.com/@numberphile). They often cover these kinds of computational number theory topics as well as a host of other really interesting mathematical tangents!